Úvod do kvantového počítání (projekt)

Kurz: Úvod do kvantového počítání (IQC), Fakulta elektrotechniky a informatiky, VŠB-TU Ostrava.

Jméno: Bc. Kryštof Šara (SAR0130)

Projekt: Simulace a realizace kvantového obvodu (Simonův algoritmus)

Zadání (EN)

Build a quantum circuit that can in a single run distinguish whether a function

$$f(\begin{Bmatrix}0, 1\end{Bmatrix}^3) \rightarrow \begin{Bmatrix}0, 1\end{Bmatrix}^3 $$

is periodic or not. Implement 2 variants of this function using a quantum oracle constructed with CNOT and X quantum gates. Verify the designed quantum circuits on a simulator and then on a real quantum computer.

The output of this work should therefore be 2 quantum circuits (one with a periodic and one with a non-periodic function) and 4 measured results (each circuit needs to be verified on a simulator and also on a quantum computer). At the end of the work it is necessary to evaluate the measured results.

Řešení

Simulace a spouštění na reálném kvantovém počítači byly realizovány pomocí portálu IBM Quantum Learning (dostupné na adrese quantum.ibm.com/composer).

Pro řešení se nabízí hned dva algoritmy, a to Deutsch–Jozsa, a Simon. Prvním algoritmem by bylo možné nalézt, zda je funkce vyvážená (tj. na polovině funkčních hodnot je výstupem 1, na polovině druhé 0). Zadání však explicitně zmiňuje periodicitu, kterou umí zpracovat algoritmus Simonův. [1]

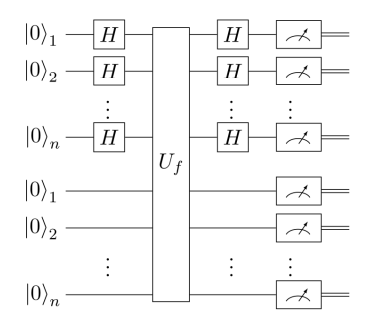Obr. 1: Simonův algoritmus (obvod).

Periodická funkce

Periodická funkce je taková, u níž se pravděpodobnosit frekvencí výpočetních 3-bitových stavů střídá s určitou periodou vzestupně od nejnižší hodnoty stavu po nejvyšší jak znázorňuje obrázek 3. Na obrázku 2 je zobrazeno rozložení kvantových bran (uvnitř bariér pouze CNOT/CX brány).

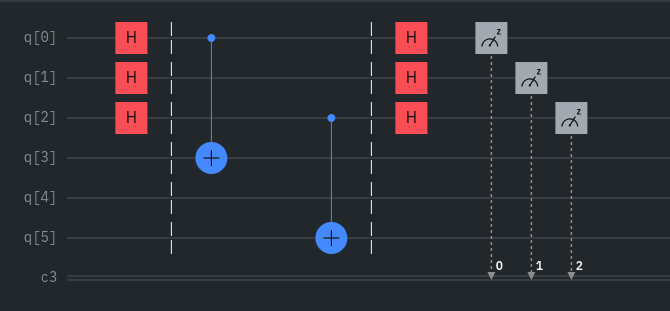Obr. 2: Kvantový obvod zjišťující periodickou funkci pomocí Simonova algoritmu.

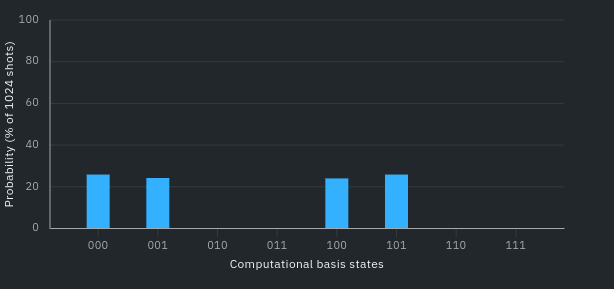Obr. 3: Histogram pravděpodobností frekvencí výsledných výpočetních 3-bitových stavů (zřetelný periodický vzor).

Obvod byl následně zrealizován na reálném kvantovém počítači firmy IBM pomocí portálu IBM Quantum Learning. Výsledek frekvencí jednotlivých výpočetních 3-bitových stavů je na obrázku 4.

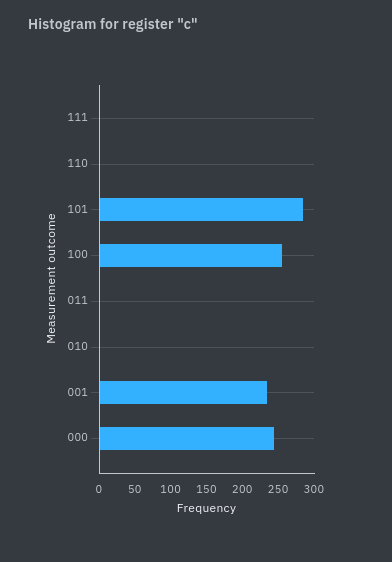Obr. 4: Výsledek reálné realizace kvantového obvodu zjišťující periodickou funkci pomocí Simonova algoritmu na kvantovém počítači.

Neperiodická funkce

Neperiodická funkce naproti tomu, jaká je situace u periodické funkce, vykazuje známky značné neperiodicity, tj. v histogramu pravděpodobností frekvencí výsledných 3-bitových stavů (obr. 6) není žádný periodický vzorec, ve kterém by se střídaly nenulové a nulové hodnoty. Všechny stavy mají nenulovou pravděpodobnost, dle simulace (obr. 6) dokonce relativně stejnou. Kvantový obvod sestavený pomocí kvantových bran (uvnitř bariér) CNOT/CX a X je zobrazen na obrázku 5.

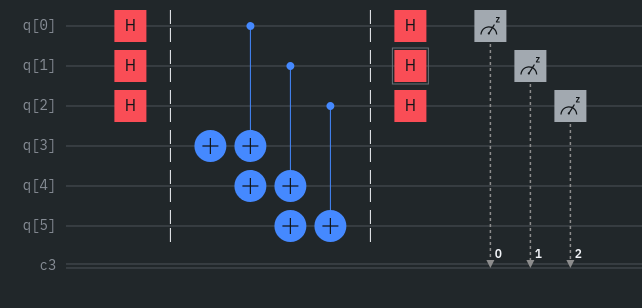Obr. 5: Kvantový obvod zjišťující neperiodickou funkci pomocí Simonova algoritmu.

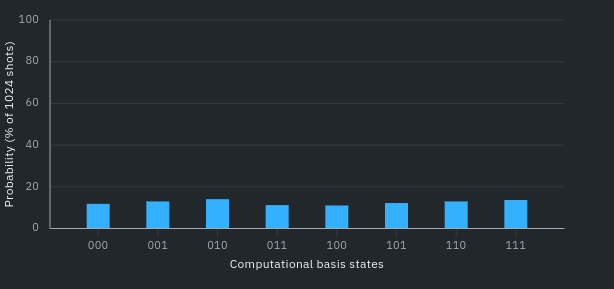*Obr. 6: Histogram pravděpodobností frekvencí výsledných výpočetních 3-bitových stavů (neperiodická funkce).

Stejně jako v předchozím případě byl kvatový obvod spuštěn na reálném kvantovém počítači společnosti IBM. Výsledek měření je na obrázku 7. V histogramu jsou vidět větší frekvence měření u stavů, u kterých paradoxně předpoklad (obr. 6) ukazoval pravděpodobnosti měnší (především stavy 011 a 100). Nutno však podotknout, že počty frekvencí měření jsou zhruba poloviční oproti předchozí variantě obvodu, jelikož jsou zde zastoupeny všechny 3-bitové stavy, které mají navíc všechny nenulový počet měření.

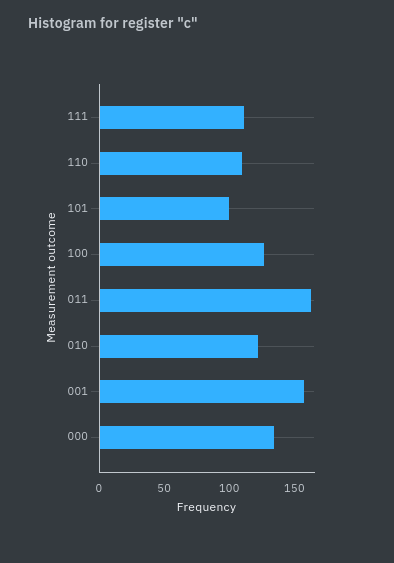Obr. 7: Výsledek reálné realizace kvantového obvodu zjišťující neperiodickou funkci pomocí Simonova algoritmu na kvantovém počítači.

Závěr

Cílem projektu bylo zhodnocení předpisu funkce a jejích vlastností (zde právě případná (ne)periodicita) a následné praktické aplikování jednoho z vhodných kvantových algoritmů, který hledané vlastnosti dokáže rozlišit. Pro konkrétní zadání tohoto projektu byl vybrát algoritmus Simonův, jelikož jako jediní z úzkého výběru základních kvantových algoritmů vyšetřuje právě periodicitu N-qubitové funkce.

Pro obě varianty periodicity byly sestaveny v prostředí IBM Qiskit kvantové obvody, jež byly vyhodnoceny z hlediska simulace (pravděpodonosti frekvencí výsledných měření stavů) a reálného dávkového spuštění na kvantovém počítači, kde bylo zapsáno 1024 měření, výstupů algoritmu. V prvním případě (periodická funkce) se histogramy blížily svými výsledky jak v případě simulace, tak i měření. V případě neperiodické funkce byly změřené výsledky lehce odlišné od těch ze simulace, avšak z hlediska neperiodického vzoru to spíše napomohlo označení takového výsledku pro neperiodicitu.

Reference