
Kurz: Pravděpodobnost a statistika (PaSTA)
Projekt č. 1: Pravděpodobnost I
Jméno: Bc. Kryštof Šara (SAR0130)
Datum: 25. 03. 2025
Příklad 1
Zadání
Termín pro odevzdání diplomové práce je 30. 4. Mirek nerad pracuje se zbytečným předstihem a tak v tento den musí svou práci ještě dopsat, vytisknout a nechat na počkání svázat v knihařství, kam může včas dojet pouze autem. Pravděpodobnost, že se v tento den pokazí počítač, na kterém svou práci píše, je 0,05. Pravděpodobnost, že se pokazí tiskárna je 0,2. Naštěstí má ještě druhou tiskárnu, které ale s pravděpodobností 0,3 dojde toner a náhradní není k dispozici. Auto je sice spolehlivé, ale s pravděpodobností 0,08 překousala kuna elektrické kabely. Knihař na rozdíl od auta úplně spolehlivý není, s pravděpodobností 0,15 práci během vázání zničí. Určete s jakou pravděpodobností Mirek práci včas odevzdá.
Řešení
Nejdříve si vypíšeme jednotlivé jevy a doplňky těchto jevů.
$$ \begin{align} &P \dots \text{pokazí se počítač},~\overline{P} \dots \text{nepokazí se počítač}\\ &T1 \dots \text{pokazí se první tiskárna},~\overline{T1} \dots \text{nepokazí se první tiskárna}\\ &T2 \dots \text{dojde toner druhé tiskárně},~\overline{T2} \dots \text{nedojde toner druhé tiskárně}\\ &K \dots \text{kuna překouše kabely v autě},~\overline{K} \dots \text{kuna nepřekouše kabely v autě}\\ &Z \dots \text{knihař zničí vázání práce},~\overline{Z} \dots \text{knihař nezničí vázání práce}\\ &O \dots \text{Mirek odevzdá práci včas} \end{align} $$
Dále si ze zadání vypíšeme pravděpodobnosti jednotlivých jevů a pravděpodobnosti doplňků, a to tak, že
$$ P(X) \dots \text{pravděpodobnost jevu X},~P(\overline{X}) \dots \text{pravděpodobnost doplňku jevu X.} $$
$$ P(P) = 0.05,~P(\overline{P}) = 1 - P(P) = 0.95\\ P(T1) = 0.20,~P(\overline{T1}) = 1 - P(T1) = 0.80\\ P(T2) = 0.30,~P(\overline{T2}) = 1 - P(T2) = 0.70\\ P(K) = 0.08,~P(\overline{K}) = 1 - P(K) = 0.92\\ P(Z) = 0.15,~P(\overline{Z}) = 1 - P(Z) = 0.85\\ \\ P(O) = ? $$
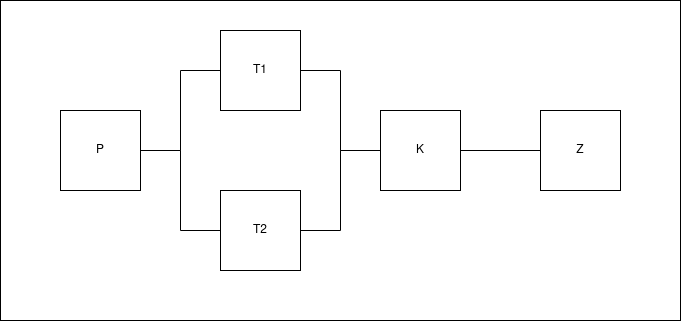 Obr. 1: Diagram se zobrazením sériovosti a paralelnosti jednotlivých jevů pro zadání 1.
Obr. 1: Diagram se zobrazením sériovosti a paralelnosti jednotlivých jevů pro zadání 1.
Jevy \(T1\) a \(T2\) je nutné sloučit v grafu (obrázek 1) do paralelního svazku. Průnik doplňků těchto jevů (tedy, že alespoň jedna tiskárna funguje) pak označíme jako pravděpodobnost \(P(\overline{T})\), přičemž jev \(\overline{T}\) značí:
$$ \begin{align} &\overline{T} \dots \text{alespoň jedna tiskárna funguje}\\ \end{align} $$
$$ P(\overline{T}) = P(\overline{T1} \cup \overline{T2}) = 1 - P(T1 \cap T2) $$
Pokud předpokládáme nezávislost jevů, můžeme rovnou pravděpodobnost průniku jevů \(T1\) a \(T2\) psát jako jejich součin, tedy součin pravděpodobností jednotlivých jevů rovnou ze zadání:
$$ P(\overline{T}) = 1 - P(T1 \cap T2) = 1 - P(T1) * P(T2) = 1 - 0.20 * 0.30 = 1 - 0.06 = 0.94 $$
Dále můžeme díky sériovosti diagramu rovnou psát výslednou pravděpodobnost \(P(O)\), tedy že Mirek odevzdá práci včas, jako průnik doplňků jednotlivých jevů a sjednocené pravděpodobnosti tiskáren:
$$ P(O) = P(\overline{P} \cap \overline{T} \cap \overline{K} \cap \overline{Z}) $$
$$ \boxed{ P(O) = P(\overline{P}) * P(\overline{T}) * P(\overline{K}) * P(\overline{Z}) = 0.95 * 0.94 * 0.92 * 0.85 \approx 0.70 } $$
Pravděpodobnost, že Mirek odevzdá svou práci všas, je přibližně 0.70.
Příklad 2
Zadání
Filtr nevyžádané pošty obsahuje databázi frází, které se ve spamu vyskytují s vysokou četností. Analýzou bylo zjištěno, že pokud je daný email spam, pak s pravděpodobností 0,9 obsahuje nějakou frázi z databáze. V případě, že se nejedná o spam, je v těle emailu nějaká fráze z databáze s pravděpodobností 0,05. Dále je známo, že 40 % emailů, které přichází na server, tvoří spam.
- a) Jaká je pravděpodobnost, že příchozí email obsahuje frázi z databáze?
- b) Jaká je pravděpodobnost, že příchozí email obsahující frázi z databáze je spam?
Řešení
Nejprve si vypíšeme jednotlivé jevy ze zadání:
$$ \begin{align} &S \dots \text{příchozí mail je spam},~\overline{S} \dots \text{příchozí mail není spam}\\ &F \dots \text{příchozí mail obsahuje frázi z databáze},~\overline{F} \dots \text{příchozí mail neobsahuje frázi z databáze}\\ \end{align} $$
Dále zadání poukazuje na podmíněné pravděpodobnosti, a to:
$$ P(F \vert S) \dots \text{pokud je daný mail spam, tak obsahuje nějakou frázi z databáze}\\ P(F \vert \overline{S}) \dots \text{pokud není daný mail spam, tak obsahuje nějakou frázi z databáze}\\ $$
Ze zadání můžou být vypsány jednotlivé pravděpodobnosti:
$$ P(F \vert S) = 0.90\\ P(F \vert \overline{S}) = 0.05\\ P(S) = 0.40 \implies P(\overline{S}) = 0.60 \\ $$
Ze zadání ještě vyplývají jednotlivá podzadání, tedy:
$$ a) P(F) = ?\\ b) P(S \vert F) = ?\\ $$
Podřešení a)
Pomocí Bayesova vzorce lze jednotlivé složené pravděpodobnosti rozepsat přímo jako:
$$ P(F) = P(F \vert \overline{S}) * P(\overline{S}) + P(F \vert S) * P(S) $$
Hodnoty pravděpodobností je možné psát přímo ze zadání a z dopočteného doplňku \(P(\overline{S})\):
$$ \boxed{ P(F) = 0.05 * 0.60 + 0.90 * 0.40 \approx 0.39 } $$
Pravděpodobnost, že příchozí mail obsahuje frázi z databáze, je přibližně 0.39.
Podřešení b)
Opět lze použít Bayesův vzorec, tedy přímo jako:
$$ P( S \vert F ) = \frac{ P(S \cap F) }{ P(F) } = \frac{ P(F \vert S) * P(S) }{ P(F) } $$
Předpokládáme, že jevy \(S\) a \(F\) jsou nezávislé, pak lze rozepsat průnik v čitateli jako součin pravděpodobností jednotlivých jevů.
Pravděpodobnost, že příchozí mail obsahuje frázi z databáze, byla vypočtena v předchozím podřešení/podpříkladu, tj.:
$$ P(F) \approx 0.39 $$
Dosazením hodnot pak:
$$ \boxed{ P( S \vert F ) = \frac{ 0.90 * 0.40 }{ 0.39 } \approx 0.92 } $$
Pravděpodobnost, že příchozí mail obsahující frázi z databáze je spam, je přibližně 0.92.