
Kurz: Funkce komplexní proměnné a integrální transformace (FKPIT)
Projekt č. 1: Fourierovy řady, Zadání č. 8
Jméno: Bc. Kryštof Šara (SAR0130)
Datum: 30. 11. 2023
Zadání
Buď \(T = 5\) a buď \(f\) taková \(T\)-periodická funkce, že platí: $$ f(t) = \begin{cases} -2e^{-3t}, & t \in \lbrack0, 3), \\ 0, & t \in [3,5). \ \end{cases} $$
- Sestavte Fourierovou řadu funkce \(f\)
- Sestavte sinovou Fourierovou řadu funkce \(f\) v intervalu \((0, T)\)
- Sestavte kosinovou Fourierovou řadu funkce \(f\) v intervalu \((0,T)\)
- V každém z případů nakreslete:
- graf součtu příslušné Fourierovy řady,
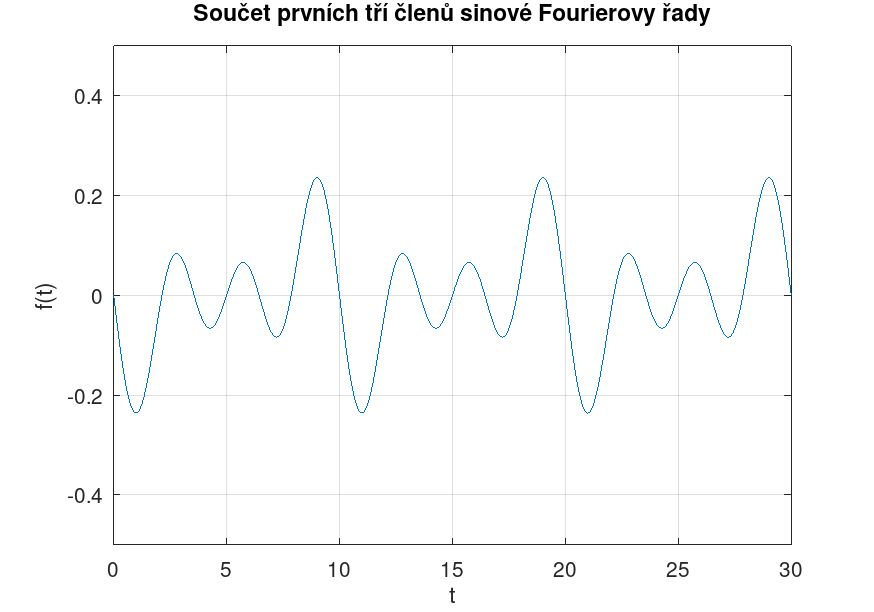
- graf součtu prvních tří členů Fourierovy řady,
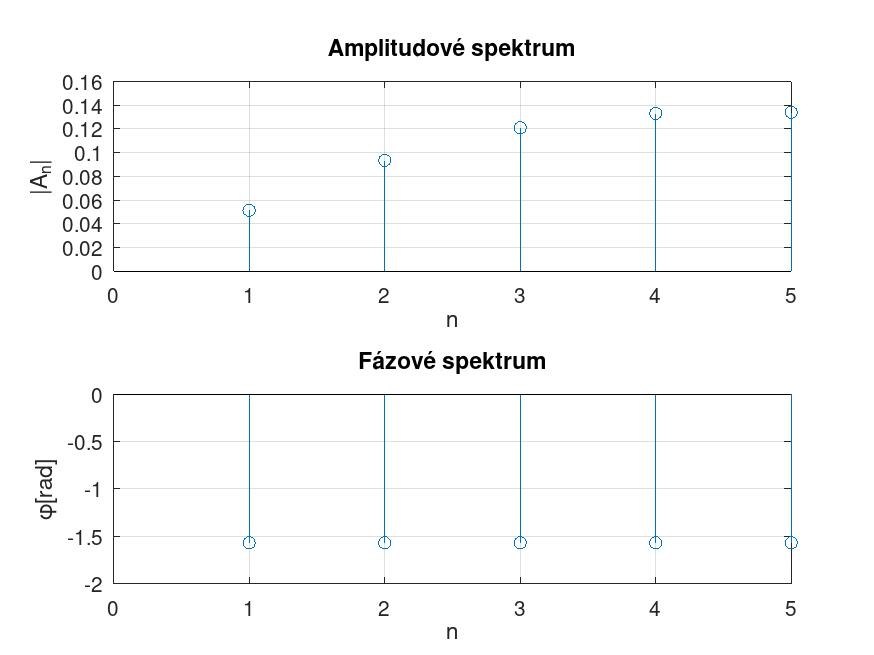
- prvních pět členů fázového a amplitudového spektra.
Analýza
Dirichletovy podmínky [1]
- funkce \( f(t) \) je periodická,
- funkce \( f(t) \) má v intervalu periodicity jen konečný počet nespojitosti 1. druhu,
- funkce \( f(t) \) má v intervalu periodicity po částech spojistou derivaci.
Oveření, zda je zadaná funkce kvadraticky integrovatelná:
$$ \int_{0}^{5} \vert f(t) \vert^2 dt < \infty $$ $$ \int_{0}^{3} \vert -2e^{-3t} \vert^{2} dt + \int_{3}^{5} \vert 0 \vert^{2} dt = \frac{2}{3} - \frac{2}{3e^{18}} \approx 0,667 < \infty $$
Z výsledku je patrné, že integrál kvadrátu zadané funkce je konečný, tudíž zadaná funkce je kvadraticky integrovatelná a jsou tím splněny Dirichletovy podmínky.
Sestavení
V každém z případů nakreslete:
- graf součtu příslušné Fourierovy řady,
- graf součtu prvních tří členů Fourierovy řady,
- prvních pět členů fázového a amplitudového spektra.
Sestavení Fourierovy řady
$$ f(t) = \begin{cases} -2e^{-3t}, & t \in \lbrack0, 3), \\ 0, & t \in [3,5). \ \end{cases} $$
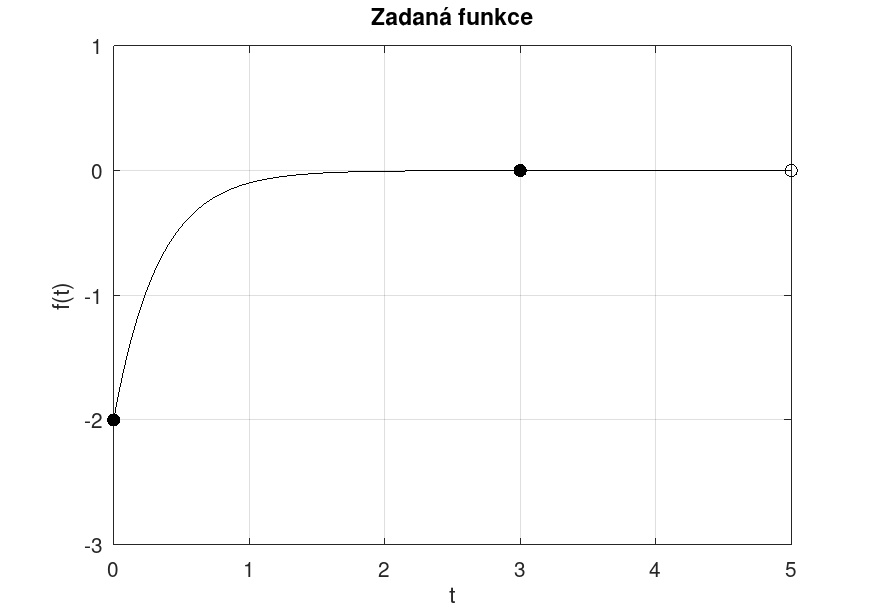
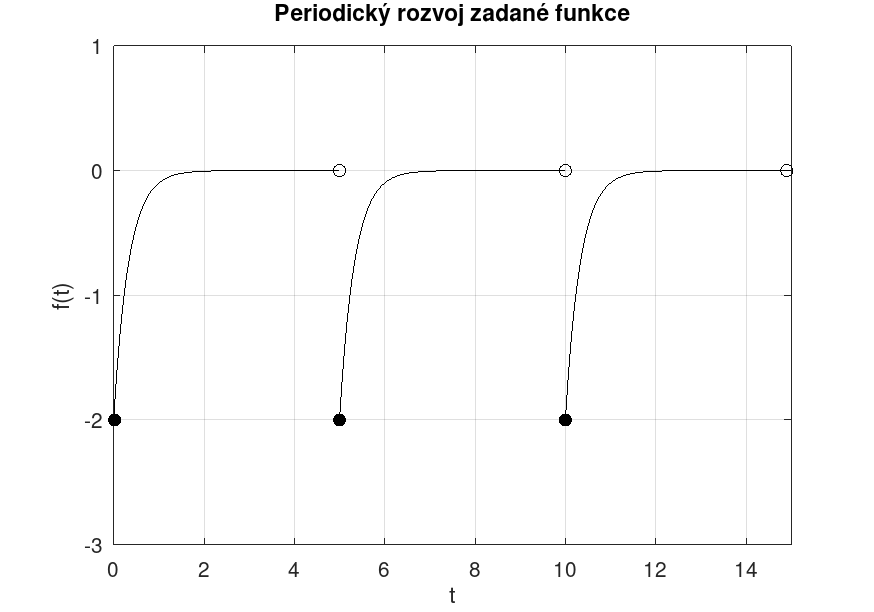
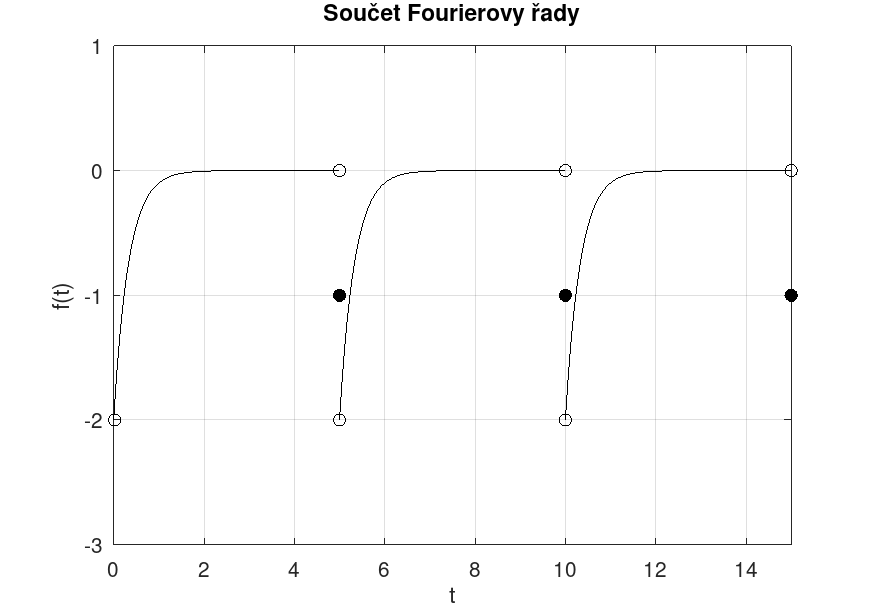
Parametry
| parametr | popis parametru |
|---|---|
| \( T = 5 \) | perioda |
| \( \omega = \frac{2\pi}{T} = \frac{2}{5}\pi \) | úhlová rychlost |
| \( L = \frac{T}{2} = \frac{5}{2} \) | půlperioda |
Koeficienty Fourierovy řady
$$ f(t) = \frac{a_0}{2} + \displaystyle\sum_{n=1}^{\infty} \lbrack {a_n cos(n\omega t) + b_n sin(n\omega t)} \rbrack $$
$$ a_0 = \frac{2}{T} \int_{0}^{T} f(t) dt $$
$$ a_n = \frac{2}{T} \int_{0}^{T} f(t) * cos(n \omega t) dt $$
$$ b_n = \frac{2}{T} \int_{0}^{T} f(t) * sin(n \omega t) dt $$
$$ c_n = \frac{1}{2} (a_n - ib_n) $$
Spektrální koeficienty
$$ A_0 = \frac{ \vert a_0 \vert }{2} $$
$$ A_n = \sqrt{ a_n^2 + b_n^2 } = 2 * \vert c_n \vert $$
$$ \varphi_n = - arg(c_n) $$
Výpočet koeficientů Fourierovy řady
Následující hodnoty byly získány pomocí výpočetního software Octave.
| \( n \) | \( a_n \) | \( b_n \) | \( c_n \) | \( A_n \) | \( \varphi_n \) [rad] | |
|---|---|---|---|---|---|---|
| 0 | -0,267 | — | -0,133 + 0i | 0,133 | — | |
| 1 | -0,227 | -0,095 | -0,113 + 0,048i | 0,246 | 2,745 | |
| 2 | -0,157 | -0,131 | -0,078 + 0,066i | 0,204 | 2,444 | |
| 3 | -0,103 | -0,130 | -0,052 + 0,065i | 0,166 | 2,243 | |
| 4 | -0,070 | -0,117 | -0,035 + 0,059i | 0,137 | 2,109 | |
| 5 | -0,049 | -0,104 | -0,025 + 0,052i | 0,115 | 2,017 |
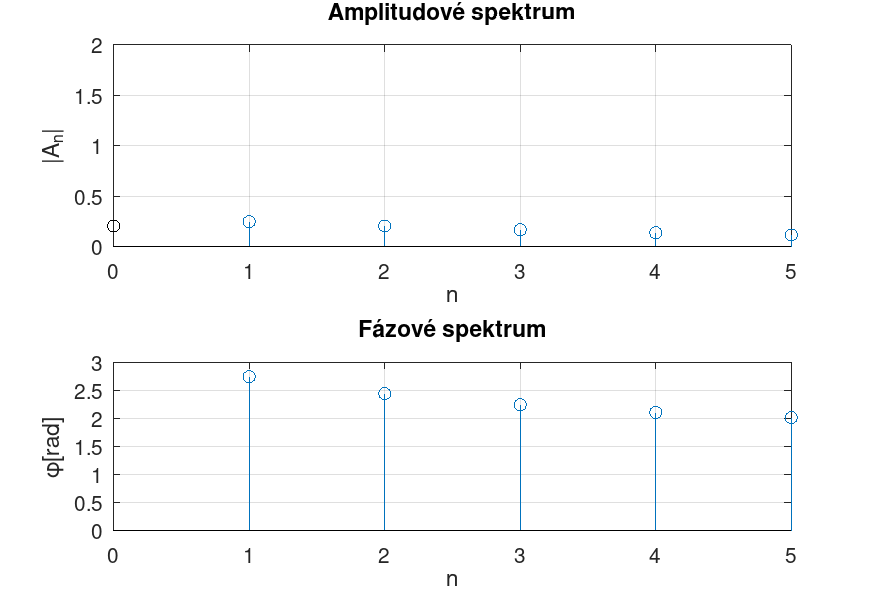
Vizualizace Fourierovy řady
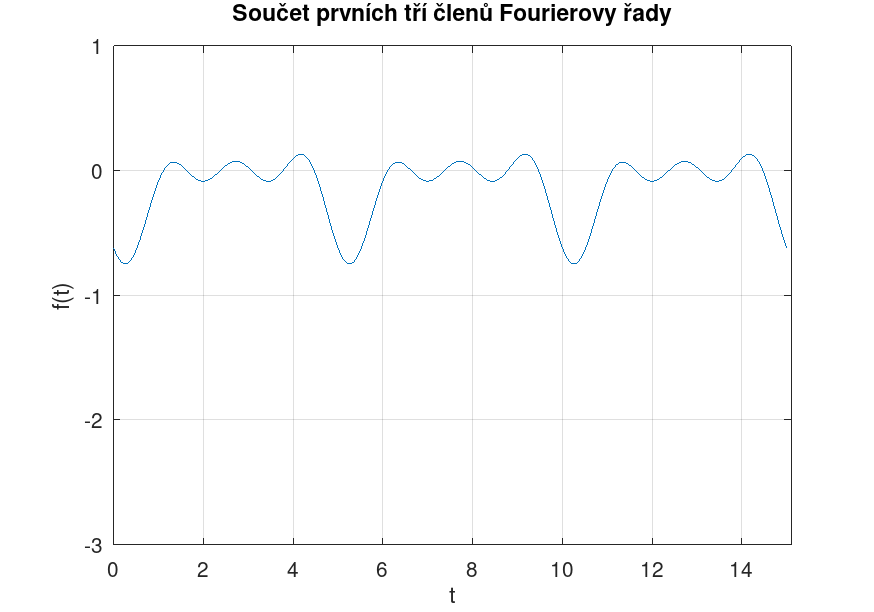
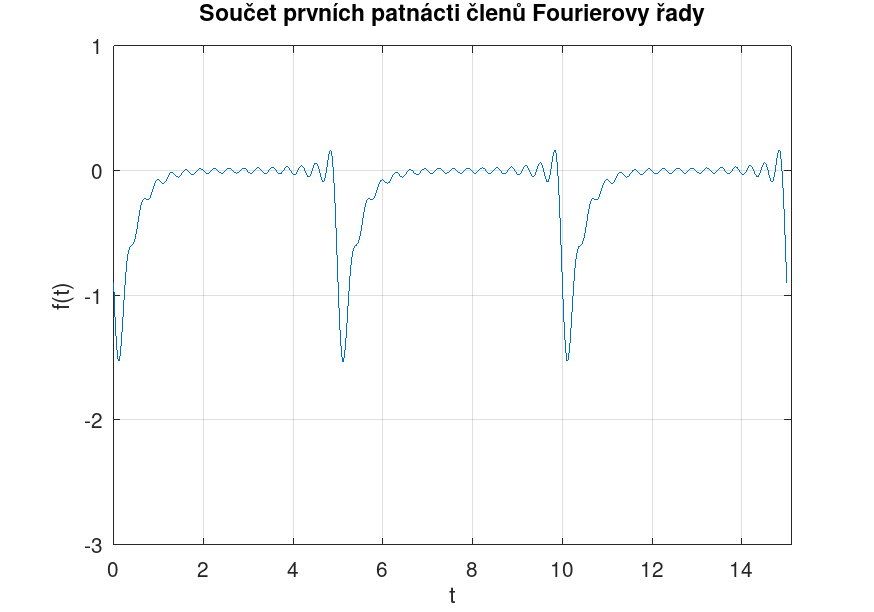
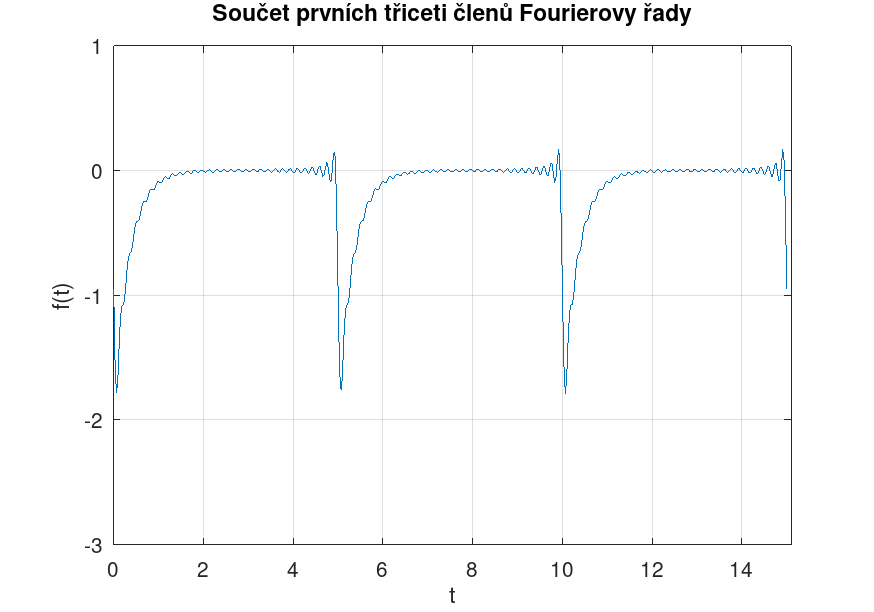
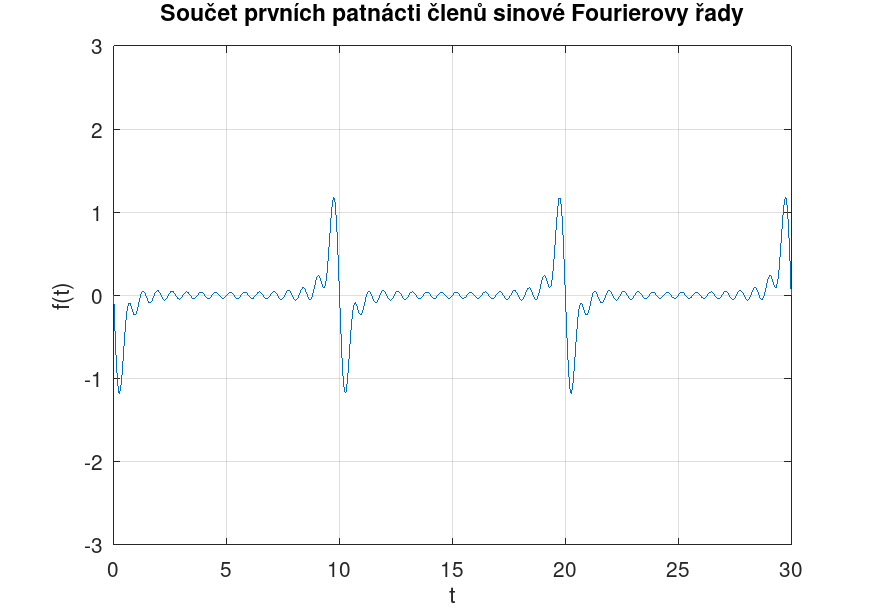
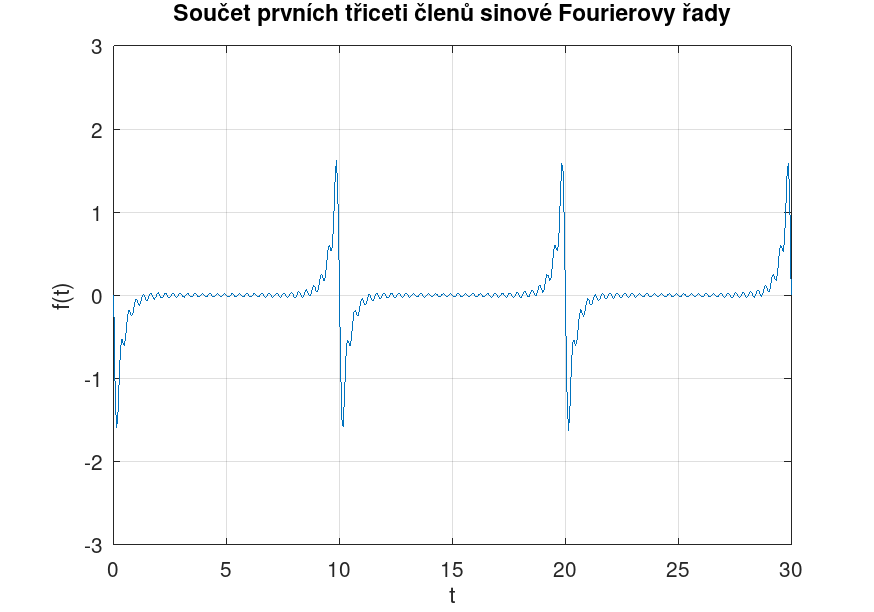
Na okrajích periody funkce \( f(t) \), která byla vyjádřena jako Fourierova řada, je patrný tzv. Gibbsův fenomén (přestřelení hodnoty funkce).
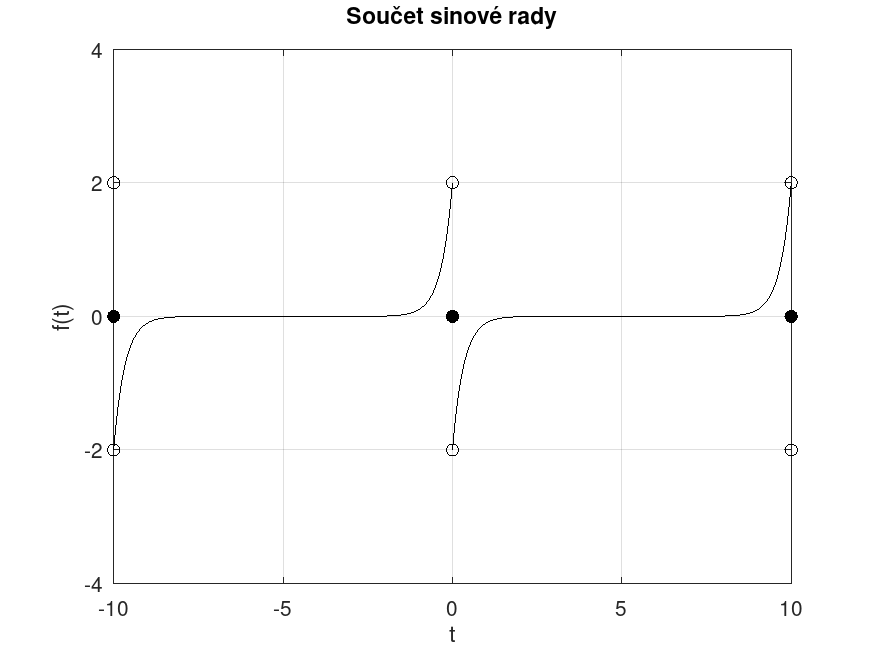
Sestavení sinové Fourierovy řady
Sinová řada budiž lichým prodloužením zadané funkce \( f(t) \), která je po částech spojitá na intervalu \( (0, T_0], T_0 = L \). Liché prodloužení se základním intervalem periodicity \( (-L, L] \) pak budiž obecně funkce \( g(t) \) a to podle předpisu: [2][4]
$$ g(t) = \begin{cases} f(t), & t \in (0, L], \\ -f(-t), & t \in (-L, 0). \ \end{cases} $$
Parametry
| parametr | popis parametru |
|---|---|
| \( T = 10 \) | perioda |
| \( \omega = \frac{2\pi}{T} = \frac{1}{5}\pi \) | úhlová rychlost |
| \( L = \frac{T}{2} = 5 \) | půlperioda |
Koeficienty sinové Fourierovy řady
$$ f(t) = \displaystyle\sum_{n=1}^{\infty} \lbrack {b_n sin(n\omega t)} \rbrack $$
$$ b_n = \frac{4}{T} \int_{0}^{T/2} f(t) * sin(n \omega t) dt $$
Spektrální koeficienty
$$ A_n = \sqrt{ b_n^2 } $$
$$ \varphi_n = arg(ib_n) $$
Hodnoty koeficientů Fourierovy řady
Následující hodnoty byly získány pomocí výpočetního software Octave.
| \( n \) | \( b_n \) | \( A_n \) | \( \varphi_n \) [rad] | |
|---|---|---|---|---|
| 1 | -0,052 | 0,052 | -1,571 | |
| 2 | -0,094 | 0,094 | -1,571 | |
| 3 | -0,120 | 0,120 | -1,571 | |
| 4 | -0,132 | 0,132 | -1,571 | |
| 5 | -0,134 | 0,134 | -1,571 |
Sestavení kosinové Fourierovy řady
Kosinová řada budiž sudým prodloužením zadané funkce \( f(t) \), která je po částech spojitá na intervalu \( (0, T_0], T_0 = L \). Sudé prodloužení se základním intervalem periodicity \( (-L, L] \) pak budiž obecně funkce \( g(t) \), a to podle předpisu: [2][4]
$$ g(t) = \begin{cases} f(t), & t \in (0, L], \\ f(-t), & t \in (-L, 0). \ \end{cases} $$
Parametry
| parametr | popis parametru |
|---|---|
| \( T = 10 \) | perioda |
| \( \omega = \frac{2\pi}{T} = \frac{1}{5}\pi \) | úhlová rychlost |
| \( L = \frac{T}{2} = 5 \) | půlperioda |
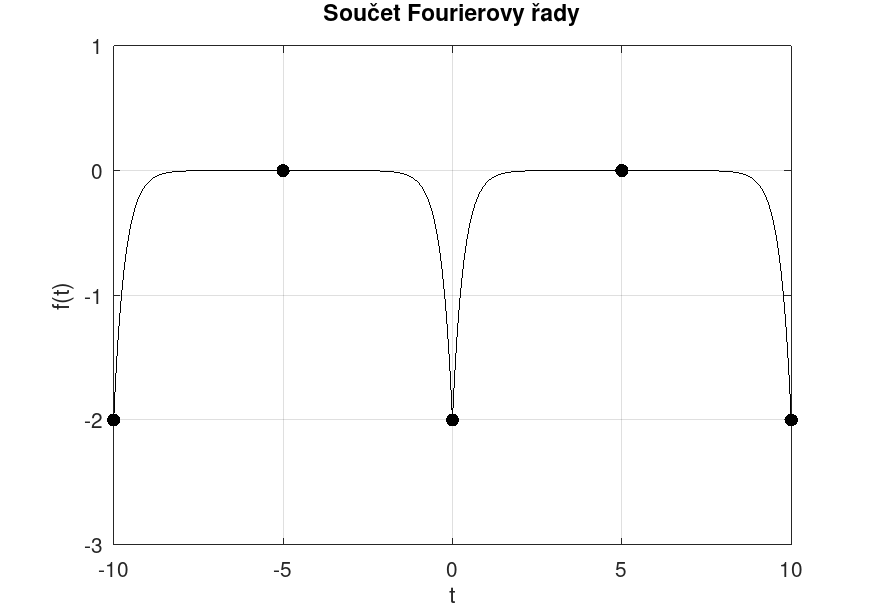
Koeficienty kosinové Fourierovy řady
$$ f(t) = \frac{a_0}{2} + \displaystyle\sum_{n=1}^{\infty} \lbrack {a_n cos(n\omega t)} \rbrack $$
$$ a_0 = \frac{4}{T} \int_{0}^{T/2} f(t) dt $$
$$ a_n = \frac{4}{T} \int_{0}^{T/2} f(t) * cos(n \omega t) dt $$
$$ c_n = \vert a_n \vert $$
Spektrální koeficienty
$$ A_n = \sqrt{ a_n^2 } $$
$$ A_0 = \frac{ \vert a_0 \vert }{2} $$
$$ \varphi_n = arg(a_n) $$
Výpočet koeficientů Fourierovy řady
Následující hodnoty byly získány pomocí výpočetního software Octave.
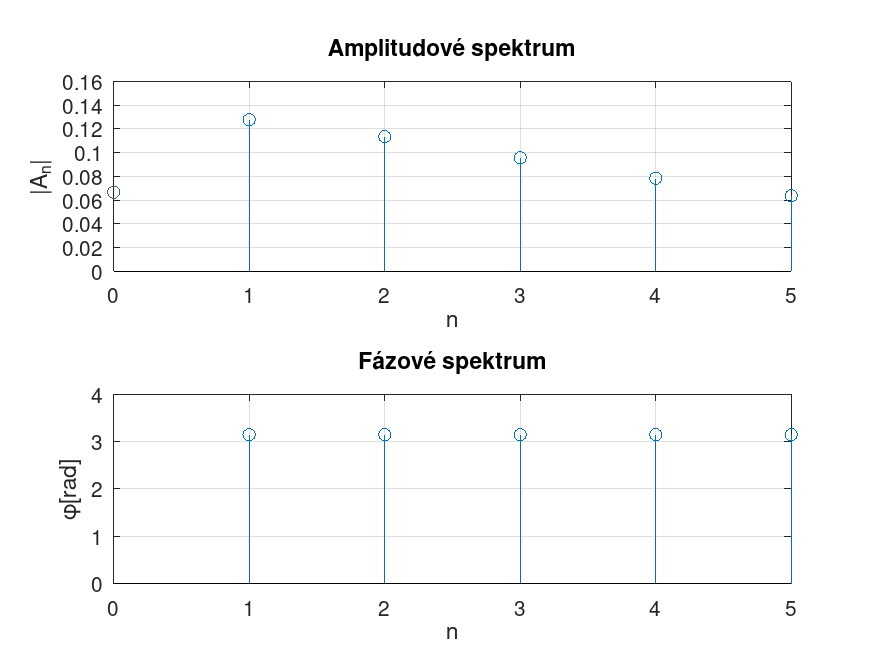
| \( n \) | \( a_n \) | \( c_n \) | \( A_n \) | \( \varphi_n \) [rad] | |
|---|---|---|---|---|---|
| 0 | -0,133 | 0,133 | 0,067 | — | |
| 1 | -0,128 | 0,128 | 0,128 | 3,142 | |
| 2 | -0,113 | 0,113 | 0,113 | 3,142 | |
| 3 | -0,096 | 0,096 | 0,096 | 3,142 | |
| 4 | -0,078 | 0,078 | 0,078 | 3,142 | |
| 5 | -0,064 | 0,064 | 0,064 | 3,142 |
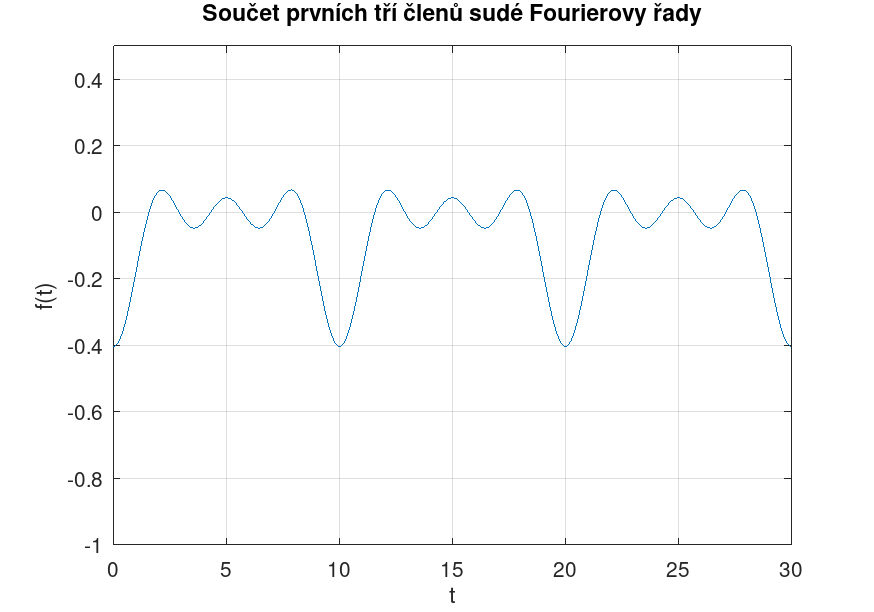
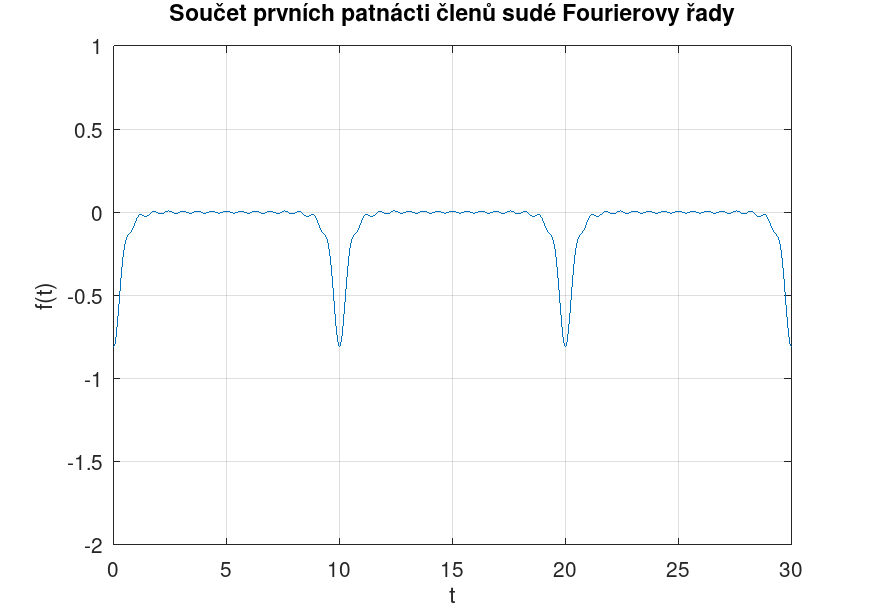
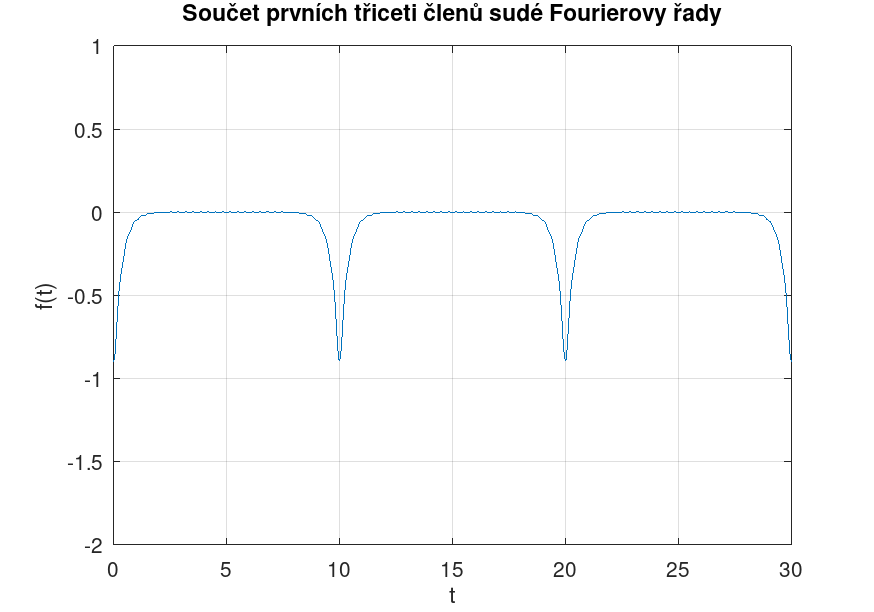
Reference
Použitý výpočetní software:
- GNU Octave 7.3.0
- Wolfram Alpha